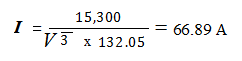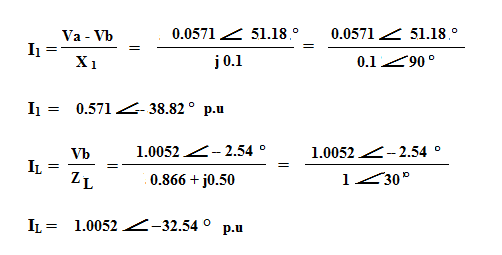8.1 Hitunglah ΔP4(0)
untuk meneruskan Contoh 8.1.
Jawab
: Nilai-nilai
Dasar untuk sistem adalah 100 MVA dan 138 kV.
Tabel 8.1
|
|||||||
Saluran antar rel
|
Panjang
|
R
|
X
|
R
|
X
|
Mvar
|
|
km
|
mi
|
Ω
|
Ω
|
p.u
|
p.u
|
Pengisian
|
|
1-2
|
64.4
|
40
|
8
|
32
|
0.042
|
0.168
|
4.1
|
1-5
|
48.3
|
30
|
6
|
24
|
0.031
|
0.126
|
3.1
|
2-3
|
48.3
|
30
|
6
|
24
|
0.031
|
0.126
|
3.1
|
3-4
|
128.7
|
80
|
16
|
64
|
0.084
|
0.336
|
8.2
|
3-5
|
80.5
|
50
|
10
|
40
|
0.053
|
0.210
|
5.1
|
4-5
|
96.5
|
60
|
12
|
48
|
0.063
|
0.252
|
6.1
|
Pengisian pada 138 kV
Tabel 8.2
|
||||||||
Rel
|
Pembangkitan
|
Beban
|
V, p.u
|
Keterangan
|
||||
P, MW
|
Q, Mvar
|
P, MW
|
Q, Mvar
|
|||||
1
|
------
|
------
|
65
|
30
|
1.04a0°
|
Rel berayun
|
||
2
|
0
|
0
|
115
|
60
|
1.00a0°
|
Rel Beban (induktif)
|
||
3
|
180
|
------
|
70
|
40
|
1.02a0°
|
Besar tegangan konstan
|
||
4
|
0
|
0
|
70
|
30
|
1.00a0°
|
Rel Beban (induktif)
|
||
5
|
0
|
0
|
85
|
40
|
1.00a0°
|
Rel Beban (induktif)
|
||
Dalam menghitung P4(0)
admitansi-admitansi yang diperlukan adalah :
Y44 = – Y43
– Y45 = – |Y43| Aθ43 – |Y45|
Aθ45
Y44 = – Y43
– Y45 = – 2.887 A104.04° – 3.850 A104.04°
Y44 = – ( –
0.7004 + j 2.8008) – ( – 0.934 + j 3.735)
Y44 = 1.6344
+ j 6.5354 = 6.737 A–75.6° = |Y44| Aθ44
Dari pers.(8.18) karena
Y41 dan Y42 = 0 , dan semua nilai-nilai awal δ(0)
= 0, maka kita sederhanakan :
P4(0)yang
dihitung = |V4V3Y43| Cosθ43 +
|V4V4Y44| Cosθ44 + |V4V5Y45|
Cosθ45
P4(0)yang
dihitung = 1x1.02x2.887 Cos104.04° + 1x1x6.737 Cos(-75.96°) + 1x1x3.850
Cos104.04°
P4(0)yang
dihitung = – 0.7144 + 1.6344 – 0.934 = – 0.0140 p.u
Daya yang ditetapkan ke
dalam rel 4 (lihat tabel 8.2)
ΔP4(0)
= – 0.70 – ( – 0.0140) = – 6.860 p.u
Keterangan : (Slack Bus no. 1, PV Bus di tukar jadi no 2,
untuk memudahkan eliminasi matriknya)
Penyelesaian Soal di atas dengan bantuan komputer , program
dibuat dalam bahasa Basica.
Hasilnya bisa diperiksa di bawah ini ( dengan Metode Fast
Decouple memerlukan iterasi ke 30 )
Bandingkan hasilnya dengan jawaban Soal 8.7 di bawah ini.
8.2 Tentukanlah nilai unsur ( ∂P3 /∂δ4 ) pada
kolom ketiga dan baris kedua dari jacobian
untuk iterasi pertama dalam meneruskan Contoh 8.1.
Jawab
: Matrik
Jacobian dari Contoh 8.1 dengan
ketentuan rel 1 berayun dan rel 3 dibuat konstan (∂δ1 dan ∂|V3|
tidak ada) adalah :
1
|
2
|
3
|
4
|
5
|
6
|
7
|
||||||
ΔP2
|
∂P2
|
∂P2
|
∂P2
|
∂P2
|
∂P2
|
∂P2
|
∂P2
|
Δδ2
|
1
|
|||
∂δ2
|
∂δ3
|
∂δ4
|
∂δ5
|
∂|V2|
|
∂|V4|
|
∂|V5|
|
||||||
ΔP3
|
∂P3
|
∂P3
|
∂P3
|
∂P3
|
∂P3
|
∂P3
|
∂P3
|
Δδ3
|
2
|
|||
∂δ2
|
∂δ3
|
∂δ4
|
∂δ5
|
∂|V2|
|
∂|V4|
|
∂|V5|
|
||||||
ΔP4
|
∂P4
|
∂P4
|
∂P4
|
∂P4
|
∂P4
|
∂P4
|
∂P4
|
Δδ4
|
3
|
|||
∂δ2
|
∂δ3
|
∂δ4
|
∂δ5
|
∂|V2|
|
∂|V4|
|
∂|V5|
|
||||||
ΔP5
|
=
|
∂P5
|
∂P5
|
∂P5
|
∂P5
|
∂P5
|
∂P5
|
∂P5
|
x
|
Δδ5
|
4
|
|
∂δ2
|
∂δ3
|
∂δ4
|
∂δ5
|
∂|V2|
|
∂|V4|
|
∂|V5|
|
||||||
ΔQ2
|
∂Q2
|
∂Q2
|
∂Q2
|
∂Q2
|
∂Q2
|
∂Q2
|
∂Q2
|
ΔV2
|
5
|
|||
∂δ2
|
∂δ3
|
∂δ4
|
∂δ5
|
∂|V2|
|
∂|V4|
|
∂|V5|
|
||||||
ΔQ4
|
∂Q4
|
∂Q4
|
∂Q4
|
∂Q4
|
∂Q4
|
∂Q4
|
∂Q4
|
ΔV4
|
6
|
|||
∂δ2
|
∂δ3
|
∂δ4
|
∂δ5
|
∂|V2|
|
∂|V4|
|
∂|V5|
|
||||||
ΔQ5
|
∂Q5
|
∂Q5
|
∂Q5
|
∂Q5
|
∂Q5
|
∂Q5
|
∂Q5
|
ΔV5
|
7
|
|||
∂δ2
|
∂δ3
|
∂δ4
|
∂δ5
|
∂|V2|
|
∂|V4|
|
∂|V5|
|
Y43 = Y34
dan semua nilai-nilai awal δ(0) = 0 :
∂P3
|
= - | V3 V4 Y34|Sin (θ34 + δ4 - δ3)
|
∂δ4
|
|
∂P3
|
= - 1.02 x 1.0 x 2.887
Sin 104.04°
|
∂δ4
|
|
∂P3
|
= - 1.02 x 1.0 x 2.887
x 0.97013
|
∂δ4
|
|
∂P3
|
= - 2.857 p.u
|
∂δ4
|
8.3 Hitunglah unsur pada kolom ketiga dan baris ketiga dari jacobian pada Contoh 8.1 untuk iterasi
pertama.
Jawab
: lihat
matrik jacobian di atas, baris ketiga dan kolom ketiga adalah ( ∂P4 /∂δ4 ), seperti
dalam Soal 8.1 :
Y41 = 0 dan Y42
= 0
Y43 = |Y43|
Aθ43
= 2.887 A104.04°
Y44 = |Y44|
Aθ44
= 6.737 A–75.6°
Y45 = |Y45|
Aθ45
= 3.850 A104.04°
8.4 Hitunglah untuk iterasi pertama unsur pada kolom keenam dan
baris ketiga dari
jacobian pada
Contoh 8.1.
Jawab
: lihat
matrik jacobian di atas, baris ketiga dan kolom keenam adalah ( ∂P4 /∂|V4| ),
seperti dalam Soal 8.1 :
Y41 = 0 dan Y42
= 0
Y43 = |Y43|
Aθ43
= 2.887 A104.04°
Y44 = |Y44|
Aθ44
= 6.737 A–75.6°
Y45 = |Y45|
Aθ45
= 3.850 A104.04°
8.5 Gambarkanlah sebuah diagram seperti dalam Gambar 8.3 untuk rel
3 pada sistem dalam Contoh 8.1 dari keterangan yang diberikan oleh hasil-cetak
aliran daya dalam Gambar 8.2. Berapakah ketidakserasian (mismatch) megawatt dan
megavar yang terlihat pada rel ini?
Jawab
:
44.59 + j 35.65 + 40.46
+ j 18.06 + 24.95 + j 16.58 + 70.0 + j 40.0 = 180 + j 110.29
Bandingkan dengan
gambar di atas :
180 – 180 = 0 ; 110.3 – 110.29 = 0.01 ;
Jadi
Ketidakserasian (mismatch) = 0 + j 0.01 p.u
8.6 Salinlah Gambar 8.20 dan tunjukkan pada
gambar itu untuk Contoh 8.1 nilai-nilai dari
(a). P dan Q yang keluar dari rel 5 pada saluran 5 – 4.
(b).Q yang dicatu oleh kapasitansi tetap dari π
nominal saluran 5 – 4 pada rel 5 (Ingatlah
bahwa nilai Q ini berubah-ubah sesuai dengan |V5|2 ).
(c). P dan Q pada kedua ujung-ujung bagian seri dari π
nominal saluran.
(d). Q yang dicatu oleh kapasitansi tetap dari π
nominal saluran 5 – 4 pada rel 4.
(e). P dan Q ke dalam
rel 4 pada saluran 5 – 4.
Jawab
:
Lihat Gambar 8.2 pada hal.223 dalam buku analisa
sistem tenaga listrik :
(a). P dan Q yang
keluar dari rel 5 ke saluran 5 – 4
adalah S = 32.03 + j 8.77 MVA
(e). P dan Q yang masuk
dari saluran 5 – 4 ke rel 4 adalah S = 31.25 + j 11.09 MVA
(b). Q yang dicatu oleh
kapasitansi tetap dari π nominal saluran 5 – 4
pada rel 5.
Mvar pengisian saluran
5-4 adalah 6.1 pada rel 5 ;V5 = 0.968 p.u (6.1/2) (0.968)2
= 2.86
(d). Q yang dicatu oleh kapasitansi tetap dari π
nominal saluran 5 – 4 pada rel 4.
Mvar pengisian saluran
5-4 adalah 6.1 pada rel 5 ;V4 = 0.920 p.u (6.1/2) (0.920)2
= 2.58
(c). P dan Q pada kedua
ujung-ujung bagian seri dari π nominal saluran.
Di ujung keluar rel 5
adalah S = 32.03 + j ( 8.77 + 2.86) = 32.03 + j 11.63 MVA
Di ujung masuk rel 4
adalah S = 31.25 + j (11.09 – 2.58) = 31.25 + j 8.51 MVA
8.7 Sebagai bagian dari penyelesaian aliran
beban dari Contoh 8.1 komputer memberikan rugi saluran total sebesar 9.67 MW.
Bagaimanakah hasil ini dibandingkan dengan jumlah rugi-rugi yang dapat
diperoleh dari pencatatan aliran beban dari setiap saluran sendiri-sendiri ?
Jawab
:
Tabel Aliran Beban
|
|||
Saluran
|
Ke dalam
|
Dicatu oleh
|
Rugi
|
Saluran
|
Saluran
|
||
MW
|
MW
|
MW
|
|
1-2
|
73,98
|
71,41
|
2,57
|
1-5
|
95,68
|
92,59
|
3,09
|
3-2
|
44,59
|
43,59
|
1,00
|
3-4
|
40,46
|
38,74
|
1,72
|
3-5
|
24,95
|
24,44
|
0,51
|
5-4
|
32,03
|
31,25
|
0,78
|
J u m l a h
|
9,670
|
||
8.8 Pengaruh penguatan medan yang telah
dibicarakan dalam bagian 6.4 sekarang dapat dihitung. Tinjaulah sebuah
generator yang mempunyai reaktansi serempak sebesar 1.0 p.u dan terhubung ke
suatu sistem yang besar. Resistansi dapat diabaikan. Jika tegangan rel adalah
1.0A0°
p.u dan generator itu mencatu arus sebesar 0.8 p.u dengan faktor daya 0.8
tertinggal pada rel, hitunglah besar dan sudut tegangan Eg dari generator dalam keadaan tanpa-beban, serta P dan Q yang
diberikan pada rel. Kemudian carilah sudut δ antara Eg dan tegangan rel, arus Ia,
dan Q yang diberikan pada rel oleh generator, jika keluaran daya generator
tetap konstan tetapi penguatan generator (a). diturunkan sehingga |Eg| menjadi 15 % lebih kecil dan (b). dinaikkan sehingga|Eg| menjadi 15 % lebih besar. Berapa persenkah perubahan pada
Q dengan penurunan dan kenaikan |Eg|
itu ?. Apakah hasil-hasil soal ini sesuai dengan kesimpulan-kesimpulan yang
dicapai dalam bagian 6.4 ?
Jawab
:
| Vt |∙|
Ia | Cos θ ; faktor daya 0.8 tertinggal
; Cos θ = 0.8 è θ = 36.87° ; Sin θ = 0.6
Vt = 1.0 A0°
; Ia = 0.8 A-
36.87° = 0.8 ( 0.8 – j 0.6) = 0.64 – j 0.48
Eg = Vt + j
Ia .Xg = 1.0 +
(0.64 – j 0.48) . j 1.0 = 1.0 + j0.64 + 0.48
Eg
= 1.48 + j0.64 = 1.6125 A23.4° p.u
P + jQ = | Vt |∙|
Ia | Cos θ = 1.0 (0.64 – j0.48) = (0.64 – j 0.48)
p.u
P
= 0.64 p.u diberikan ke rel; Q = 0.48 p.u diberikan ke rel
(a). diturunkan hingga 15%
; |Eg|baru = (100-15)% x 1.6125 = 0.85 x 1.6125 =
1.370 p.u
(b). dinaikkan hingga 15%
; |Eg|baru = (100+15)% x 1.6125 = 1.15 x 1.6125 =
1.854 p.u
Kesimpulan :
Menurunkan eksitasi
generator berarti menurunkan Q yang diserahkan dan menaikkan eksitasi generator
berarti menaikkan Q yang diserahkan.
8.9 Suatu sistem daya dimana dihubungkan
sebuah generator pada sebuah rel tertentu dapat disajikan sebagai tegangan Thevenin Eth = 0.9A0° p.u dalam hubungan
seri dengan Zth =
0.25A90°
p.u . Bila dihubungkan pada sistem ini, Eg
dari generator adalah 1.4 A30° p.u. Reaktansi serempak
generator dengan dasar sistem itu adalah 1.0 p.u. (a). Hitunglah tegangan Vt dan P dan Q yang dipindahkan
ke dalam sistem pada rel; (b). Jika tegangan rel akan dinaikkan menjadi | Vt | = 1.0 p.u untuk P yang sama yang dipindahkan ke sistem,
hitunglah nilai Eg yang
diperlukan dan nilai Q yang
dipindahkan ke sistem pada rel. Misalkanlah bahwa emf-emf yang lain dalam
sistem tidak berubah besar dan sudutnya; yang berarti bahwa Eth dan Zth konstan.
Jawab
:
I = 0.56 – j0.25 = 0.613 A-24.06°
p.u
Vt = Eth
+ Zth . I
Vt = 0.9 + j
025 ( 0.56 – j0.25) = 0.9 + 0.0625 + j0.14
Vt
= 0.9625 + j0.14 = 0.973 A8.28° p.u
P + j Q = Vt
. I*
P + j Q = 0.973 A8.28°
x 0.613 A24.06°
= 0.596 A32.34°
P
+ j Q = 0.504 + j 0.318 p.u
P
= 0.504 p.u dan Q = 0.318 p.u yang dipindahkan ke rel.
I = 0.56 – j0.36 =
0.665 A-32.7°
p.u
Eg = Vt + Xg . I
Eg = 0.990 + j0.14 +
j1.0 (0.56 – j0.36) = 0.990 + j0.14 +
j0.56 + 0.36
Eg
= 1.35 + j 0.70 = 1.52 A27.4° p.u
P + j Q = Vt . I*
P + j Q = 1.0 A8.05°
x 0.665 A32.7°
= 0.665 A40.75°
P
+ j Q = 0.504 + j 0.434 p.u
P
= 0.504 p.u dan Q = 0.434 p.u yang dipindahkan ke rel.
8.10 Dalam Soal 7.10 tegangan-tegangan pada
ketiga rel dihitung sebelum dan sesudah pemasangan sebuah kapasitor dari netral
ke rel 3. Tentukanlah P dan Q yang memasuki atau meninggalkan rel 3 lewat
saluran-saluran transmisi, melalui reaktansi yang terhubung antara rel dan
netral, dan dari kapasitor sebelum dan sesudah kapasitor dipasang. Misalkan
bahwa tegangan-tegangan yang dibangkitkan tetap konstan besar dan sudutnya.
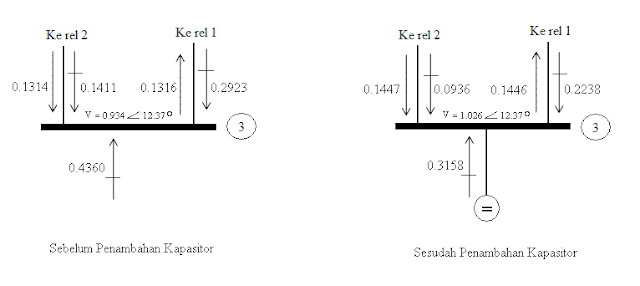
Gambarkanlah diagram-diagram seperti dalam Gambar 8.9 untuk menunjukkan
niali-nilai yang telah dihitung.
Jawab
:
Sebelum
penambahan Kapasitor
Dari jawaban Soal 7.10
diperoleh :
V1 = 0.980 +
j0.186 = 0.997 A10.75° p.u
V2 = 0.959 +
j0.268 = 0.996 A15.61° p.u
V3 = 0.912 +
j0.200 = 0.934 A12.37° p.u
Dalam reaktansi shunt
pada simpul (3)
Q = (V3)2/X3-0
= (0.934)2/2.0 = 0.436 p.u
Kedalam rel 3 dari rel 1 :
Sesudah
penambahan Kapasitor
Dari jawaban Soal 7.10 diperoleh :
V1 = 1.0509
+ j0.2016 = 1.070 A10.86° p.u
V2 = 1.0257
+ j0.2826 = 1.064 A15.41° p.u
V3 = 1.0022
+ j0.2198 = 1.026 A12.37° p.u
Dalam shunt XL dan
XC pada simpul (3)
Perhatikan bahwa P ke rel 3 harus sama dengan nol
terbukti benar, kecuali ada selisih dalam hal pembulatan-pembulatan :
- 0.1316 + 0.1314 = - 0.0002 dan
- 0.1446 + 0.1447 = 0.0001
8.11 Gambar 8.9 menunjukkan bahwa 15.3 Mvar
harus dicatu oleh suatu bangku kapasitor pada rel 4 dalam sistem 60-Hz dari
Contoh 8.1 untuk menaikkan tegangan rel menjadi 0.950 p.u. Jika tegangan dasar
adalah 139 kV, hitunglah kapasitansi pada setiap fasa jika kapasitor-kapasitornya
(a). dihubungkan secara Y dan (b). dihubungkan secara Δ.
Jawab :
Gambar 8.9
Tegangan
rel = 0.95 x 139 = 132.05 kV
a). Hubungan Bintang :
b). Hubungan Delta :
Xc
= 3 x 1,139.8 = 3,419.4 Ω C = ⅓ x
2.33 x 10-6 = 0,777 x 10-6 F
8.12 Dua buah rel a dan b dihubungkan
satu dengan yang lain melalui impedansi-impedansi X1 = 0.1 dan
X2 = 0.2 p.u yang paralel. Rel b adalah suatu rel beban yang mencatu arus I = 1.0 A30°
p.u. Tegangan
rel b adalah Vb = 1.0 A0°
p.u. Hitunglah P dan Q ke dalam rel b
melalui masing-masing cabang paralel itu (a). dalam rangkaian yang telah
dilukiskan, (b). Jika sebauah transformator regulasi dihubungkan pada rel b dalam saluran dengan reaktansi
yang lebih tinggi untuk memberikan suatu peningkatan sebesar 3% pada besar tegangan
ke arah beban (a = 1.03), dan (c).
jika transformator regulasi memajukan fasa dengan 2° (a = ejπ/90).
Gunakan metoda arus putar untuk bagian-bagian (b) dan (c), dan misalkan Va
disetel sedemikian rupa shingga Vb tetap konstan untuk setiap bagian
dari soal. Gambar 8.21 adalah diagram segaris yang menunjukkan rel-rel a dan b pada sistem dengan
transformator regulasi
pada tempatnya. Abaikanlah impedansi transformator itu.
Jawab :
(a).
Arus
lewat X1 :
I1 = 2/3 x 1 A–30° = 2/3 ( 0.866 – j0.5)
I1
= 0.577 – j0.333 p.u
Arus
lewat X2 :
I2 = 1/3 x 1 A–30° = 1/3 ( 0.866 – j0.5)
I2
= 0.289 – j0.167 p.u
Kedalam
rel b lewat X1 :
P
+ j Q = Vb . I1*
= (1 + j0) (0.577 + j0.333)
P
+ j Q = 0.577 + j 0.333 p.u
Kedalam
rel b lewat X2 :
P + j Q = Vb
. I2* = (1 + j0) (0.289 + j0.167)
P
+ j Q = 0.289 + j 0.167 p.u
(b). Ditingkatkan
3 % :
∆ V = 3% = 0.03 ;
I1 = 0.577 – j0.333 – (– j0.1)
I1
= 0.577 – j 0.233 p.u
I2 = 0.289 – j 0.167 + ( – j0.1)
I2
= 0.289 – j 0.267 p.u
Kedalam
rel b lewat X1 :
P
+ j Q = Vb . I1*
= (1 + j0) (0.577 + j0.2333)
P
+ j Q = 0.577 + j 0.233 p.u
Kedalam
rel b lewat X2 :
P + j Q = Vb
. I2* = (1 + j0) (0.289 + j0.267)
P
+ j Q = 0.289 + j 0.267 p.u
(c). Fasa
dimajukan 2° :
∆ V = 1 A2° – 1.0 = 0.9994 + j0.0349 – 1.0
∆ V = – 0.0006 + j0.0349
Iputar = 0.1163 + j0.002
p.u
I1 = 0.577 – j0.333 – (0.1163 + j0.002)
I1 = 0.461 – j0.335 p.u
I2 = 0.289 – j 0.267 + 0.1163 + j0.002
I2
= 0.406 – j 0.165 p.u
Kedalam
rel b lewat X1 :
P
+ j Q = Vb . I1*
= (1 + j0) (0.461 + j0.335)
P
+ j Q = 0.461 + j 0.335 p.u
Kedalam
rel b lewat X2 :
P + j Q = Vb
. I2* = (1 + j0) (0.406 + j0.165)
P
+ j Q = 0.406 + j 0.165 p.u
Bandingkan
P dan Q yang didapatkan dalam bagian-bagian (c)
dan (a).
8.13 Dua reaktansi X1 = 0,08 dan X2
= 0,12 p.u terhubung paralel di antara dua rel a dan b pada suatu
sistem daya. Jika Va = 1,05 A10° dan Vb
= 1,0 A0° p.u, berapakah
seharusnya perbandingan lilitan transformator regulasi yang akan disisipkan
dalam hubungan seri dengan X2 pada
rel b sehingga tidak ada Var yang
mengalir ke dalam rel b dari cabang
dengan reaktansi X1?
Gunakanlah metoda arus-putar, dan abaikan reaktansi transformator regulasi. P dan
Q beban serta Vb tetap konstan.
Jawab :
Dalam Reaktansi X1 :
Iab = 2.3175
a –10.56°
Iab
= 2.278 – j 0.425 p.u
Untuk
menghilangkan daya Var ke rel b lewat X1, diperlukan
sisipan transformator regulasi pada cabang X2 :
Iab putar = – j 0.425 p.u
ΔV = a – 1
ΔV = – j0.425 ( j0.08 + j0.12 ) = ( 0.034
+ 0.051 ) = 0.085
a – 1 = 0.085
a = 1.085 (ini
perbandingan gulungan transformator)
8.14 Dua buah transfomator masing-masing dengan
rating 115 Y 13,2 ∆ kV bekerja paralel untuk mencatu sebuah beban
sebesar 35 MVA, 13,2 kV dengan faktor daya 0,8 tertinggal. Transformator 1 mempunyai rating 20
MVA dengan X = 0,09 p.u, sedangkan transformator
2 ratingnya 15 MVA dengan X = 0,07 p.u. Hitunglah besarnya arus yang
mengalir melalui masing-masing transformator dalam p.u, keluaran megavoltampere
masing-masing transformator dan batasan megavoltampere beban total sehingga
tidak ada transformator-transformator tersebut yang dibebani lebih (overload).
Jika sadapan-sadapan pada transformator 1 disetel pada 111 kV untuk memberikan
suatu peningkatan tegangan sebesar 3,6 % ke arah sisi tegangan-rendah dari
transformtor itu dibandingkan dengan transformator 2 yang tetap pada sadapan
115 kV, hitunglah keluaran megavoltampere masing-masing transformator untuk
beban total asli sebesar 35 MVA, dan megavoltampere maksimum dari beban total
yang tidak akan membebani-lebih transformator-transformator itu. Gunakanlah
sebagai dasar 35 MVA, 13,2 kV pada sisi tegangan-rendah. Metoda arus putar
sudah cukup memuaskan untuk soal ini.
Jawab :
T1
Rating 20 MVA; X1 = 0.09 p.u
T2
Rating 15 MVA; X2 = 0.07 p.u
Beban
35 MVA; 13.2 kV; pf = 0.8 laging
Dengan
mengubah ke Dasar yang dipilih (35 MVA) menjadi sebagai berikut :
X1
= 0.09 x (35/20) = 0.1575 p.u
X2
= 0.07 x (35/15) = 0.1633 p.u
#2
dibebani lebih (overload), kurangi beban hingga (15/17.2)
Arus-arus
dengan beban 35 MVA adalah :
Dengan
peningkatan Tegangan sebesar 36% :
|I1 + Iputar| = |(0.407 – j0.305) + (– j0.112)| = |0.407 – j 0.417| = 0.583 p.u
|S1| = 0.583 x 1.0 x 35 = 20.405 MVA
Perbandingannya
(20.405/20) = 1.020
|I2 – Iputar| = |(0.393 – j0.245) -– (– j0.112)| = |0.393 –
j 0.133| = 0.415 p.u
|S2| = 0.415 x 1.0 x 35 = 14.525 MVA
Perbandingannya
(14.525/15) = 0.968
Perkecil beban sampai (35/1.020) = 34.3 MVA.
8.15 Jika impedansi beban pada rel b dari rangkaian yang digunakan
dalam Soal 8.12 adalah 0.886
+ j0.5 p.u dan jika Va = 1.04 A0° p.u (tegangan
Vb dan arus beban tidak ditetapkan lagi), hitunglah Vb
untuk keadaan-keadaan yng telah diberikan dalam bagian-bagian (a), (b) dan (c)
dari Soal 8.12. Dapatkanlah juga P dan Q yang masuk ke dalam rel b melalui masing-masing cabang
pararel untuk ketiga keadaan tersebut di atas. Persamaan (8.39) harus dipakai dalam soal ini, dan impedansi
beban dapat dimasukkan ke dalam Y22 pada
persamaan-persamaan admitansi simpul dari rangkaian keseluruhannya.
Jawab :
(a). Keadaan dimana a
= 10 , diselesaikan sebagai rangkaian paralel sederhana.
Gunakan
Persamaan 8.39 untuk bagian-bagian (b) dan (c).
Beban ZL = 0.866 +
j0.50 = 1.0 a 30° p.u
Z
= [( j0.1 x j0.2 ) / ( j01 + j0.2 )]
+ (0.866 + j0.50)
Z
= ( - 0.02 / 0.3 a 90° )
Z
= – (0.067 a– 90°) + 0.866 + j0.50
= j0.067 + 0.866 + j0.50
Z = 0.866 + j0.567 = 1.035 a 33.2° p.u
IL = (Va / Z)
= ( 1.04a 0° ) / ( 1.035a 3.2° ) = 1.005 a – 33.2° p.u
Vb = IL x ZL = ( 1.005 a – 33.2° ) x ( 1.0
a 30° ) = 1.005 a – 3.2° p.u
I1 =
2/3 x IL = 2/3 x 1.005 a –
33.2° = 0.670 a – 33.2° p.u
I2 = 1/3
x IL = 1/3 x 1.005 a – 33.2° = 0.335 a – 33.2° p.u
P1
+ j Q1 = Vb x I1* = 1.005 a – 3.2° x 0.670 a +
33.2° = 0.673 a 30°
P1 + j Q1 = 0.583 + j 0.337 p.u
P2
+ j Q2 = Vb x I2* = 1.005 a – 3.2° x 0.335 a
33.2° = 0.337 a 30°
P2 + j Q2 = 0.292 + j 0.169 p.u
(b). Keadaan
dimana a = 1.03
Cari
Ib = Yba + Ybb x Vb ; dimana Ib
= 0
Karena
tidak ada arus memasuki simpul b dari suatu sumber.
Dengan
meninjau hanya cabang yang mengandung X1 :
Yba = ( -1 / j0.1 )
= j10 ; Ybb = ( 1 / j0.1 )
= – j10
Dengan
meninjau hanya cabang yang mengandung X2 :
Untuk cabang Beban :
Yba = 0 ; Ybb
= 1/ ( 0.866 + j0.50 )
= 0.866 – j0.50
Untuk
rangkaian selengkapnya (seluruhnya):
Yba = j10
+ j4.854 = j14.854 ;
Ybb =
–j 10 – j 4.713 + 0.866 – j0.50 = 0.866
– j15.213
Ybb
= 15.238 a – 86.74°
Dengan
menyelesaikan untuk Vb sebagai berikut : ( Va = 1.04 a 0°)
0 = Va x Yba+ Vb x Ybb
; Vb x Ybb
= – Va x Yba
Vb = 1.014 a – 3.26° p.u
Va – Vb = 1.04 – 1.014 a– 3.26° = 1.04 – 1.012 + j0.058 =
0.028 + j0.058
Va – Vb = 0.0644 a 64.2° p.u
I2 = IL - I1 = (1.014 a –33.26°) – ( 0.64 a –25.8°)
I2 = 0.848 – j0.556 – ( 0.576 – j 0.279) =
0.848 – j0.556 – 0.576 + j0.279
I2 = 0.272 – j0.277 = 0.388 a -– 45.52° p.u
P1 + j Q1 = Vb x I1*
= (1.014 a – 3.26°) x (0.64
a +25.8°) = 0.65 a 22.54°
P1 + j Q1 = 0.60 + j0.249 p.u
P2 + j Q2 = Vb x I2*
= (1.014 a – 3.26°) x (0.388 a +45.52°) = 0.393 a 42.26°
P2 + j Q2 = 0.290 + j0.264 p.u
(c). Keadaan dimana a
= 1.0 a 2° :
Sama
seperti bagian (b) dengan hanya meninjau cabang yang mengandung X1 :
Yba = –1 / j0.1
= j0.1 ; Ybb = 1 / j0.1
= – j10
Untuk cabang beban :
Yba = 0 ; Ybb
= 1 / ( 0.866 + j0.50 ) = 0.866 – j0.50
Untuk rangkaian keseluruhan :
Yba = –
0.174 + j4.997 + j10 = – 0.174 + j14.997
= 15 a 90.66° p.u
Ybb = 0.866
– j0.50 – j5.0 – j10 = 0.866 – j15.50 = 15.52
a – 86.80°
Persamaan simpul adalah :
0 = Va x Yba+ Vb x Ybb
0 = 1.04 x 15 a 90.66° + Vb
x 15.52 a – 86.80°
Va – Vb = 1.04 – (1.0042 – j0.0455)
= 0.0358 + j0.455 = 0.0571 a 51.18° p.u
I2 = IL - I1 = (1.0052 a –32.54°) – ( 0.571 a –38.82°)
I2 = 0.8474 – j0.5407 – ( 0.4449 – j 0.3574) =
0.4025 – j0.1828
I2 = 0.442 a -– 24.43° p.u
P1 + j Q1 = Vb . I1*
= (1.0052 a – 2.54°)
(0.571 a +38.82°) = 0.57397 a 36.28°
P1 + j Q1 = 0.4627 + j0.3396 p.u
P2 + j Q2 = Vb . I2*
= (1.0052 a – 2.54°)
(0.442 a +24.43°) = 0.4443 a 21.89°
P2 + j Q2 = 0.4123 + j0.1656 p.u