KUMPULAN SOAL DAN JAWABAN ANALISIS SISTEM TENAGA LISTRIK (William D. Stevenson, Jr.) (Bab.5 Tamat)

5.11     Suatu saluran transmisi 60-Hz tiga-fasa panjangnya 250 mi. Tegangan di ujung pengirim 220 kV. Parameter-parameter saluran adalah R = 0.2 Ω/mi, X = 0.8 Ω/mi, dan Y =5.3 µ℧/mi. Carilah arus ujung pengirim jika pada saluran tidak ada beban.

Jawab :

V_S = 220000/√3 = 120017 V

Z = 250 (R + jX) = 250 ( 0.2 + j 0.8) = 50 + j 200 = 206.2 A75.96° Ω

Y = 250 x 5.3 x 10 ^{– 6} = 1.325 x 10 ^{– 3} A90° ℧

γℓ = 0.0639 + j 0.5187 

0.5187 rad = (180/π) 0.5187 = A29.72°

Persamaan 5.39

I_R = I_S Cosh γℓ - (V_S/Z_C) Sinh γℓ      untuk I_R = 0

I_S = (V_S/Z_C) (Sinh γℓ/Cosh γℓ)

e^0.0639 . e^{j 0.5187} = 1.066 A29.72° = 0.9258 + j 0.5285

e ^{- 0.0639} . e ^{–j 0.5187} = 0.9381 A- 29.72° = 0.8147 – j 0.4651

Cosh γℓ = Cosh(0.0639 + j 0.5187) = ½( e^0.0639 . e^{j 0.5187} + e ^{- 0.0639} . e ^{–j 0.5187})

Cosh γℓ = ½(0.9258 + j 0.5285 +0.8147 – j 0.4651)

Cosh γℓ = ½(1.7405 – j 0.0634) = 0.8703 – j 0.0317

Cosh γℓ = 0.8709 A2.086°

Sinh γℓ = Sinh(0.0639 + j 0.5187) = ½( e^0.0639 . e^{j 0.5187} -  e ^{- 0.0639} . e ^{–j 0.5187})

Sinh γℓ = ½(0.9258 + j 0.5285 - 0.8147 + j 0.4651)

Sinh γℓ = ½(0.1111 + j 0.9936) = 0.05885 + j 0.4968

Sinh γℓ = 0.4999 A83.62°

I_S = 322.4 A7.02°  x 0.5740 A81.53°

I_S = 185 A88.53° A

5.12     Jika beban pada saluran yang dilukiskan dalam Soal 5.11 adalah 80 MW pada 220 kV, dengan faktor daya satu, hitunglah arus, tegangan dan daya pada ujung pengirim. Misalkan bahwa tegangan ujung pengirim dibuat konstan dan hitunglah regulasi tegangan saluran untuk beban tersebut di atas.

Jawab :

Dari Soal 5.11

Zc = 394.5 A- 7.02°

Cosh γℓ = 0.8709 A2.086° =0.8703 – j 0.0317

Sinh γℓ = 0.4999 A83.62° =0.05885 + j 0.4968

V_S = V_R Cosh γℓ + I_R Z_C Sinh γℓ

V_S = 127000(0.8703 – j 0.0317) + 209.95 (394.5 A- 7.02° x 0.4999 A83.62°)
V_S = 110.528 + j 4026 + 209.95 x 197 A76.6°

V_S =  110.528 + j 4026 + 209.95 (45.65 + j 191.64)

V_S =  110.528 + j 4026 + 9594.7 + j 40276.8 = 120 122.7 + j 44302.8

V_S = 128 032 A20.24° V ke netral

|V_S|_{antar saluran}= √3 x 128.032 = 221.8 kV

I_S = I_R Cosh γℓ + (V_R/Z_C )Sinh γℓ

I_S = 209.95 (0.8703 – j 0.0317) + (127000/394.5 A- 7.02°) x 0.4999 A83.62°

I_S = 182.72 + j 6.66 + 321.9 5 A7.02° x 0.4999 A83.62°

I_S = 182.72 + j 6.66 + 163.93 A90.64°

I_S = 182.72 + j 6.66 - 1.798 + j 160.92

I_S = 180.9 + j 167.58

I_S = 246.6 A42.81° A

P_S = √3 x |V_S| x I_S Cos (20.24° - 42.81°)

P_S = √3 x 221.8 x 246.6 Cos (-22.57°)

P_S = 87 480 kW = 87.5 MW

Untuk I_R = 0 maka V_S = V_R Cosh γℓ 
|V_R| = (V_S/Cosh γℓ) = 127 000/0.8709 = 145 826 V ke netral

Regulasi ={(145.286 - 127)/127} x 100 = 14.8 %

 5.13     Ruang-jalan untuk rangkaian-rangkaian transmisi menjadi makin sulit didapatkan di daerah-daerah perkotaan dan saluran-saluran yang sudah ada sering ditingkatkan dengan mengganti penghantar-penghantarnya dengan yang lebih besar atau menambah isolasinya untuk dapat bekerja pada tegangan yang lebih tinggi. Pertimbangan panas (thermal) dan daya maksimum yang dapat dikirimkan oleh saluran adalah faktor-faktor penting yang perlu diperhitungkan. Suatu saluran 138 kV panjangnya 50 km dan tersusun dari penghantar-penghantar Partridge dengan jarak pemisah mendatar rata sebesar 5 m antara penghantar-penghantar yang berdekatan. Abaikanlah resistansi dan carilah persentase peningkatan daya yang dapat dikirimkan untuk │V_S │dan │V_R│ yang konstan sedangkan δ dibatasi pada 45° dan (a) jika penghantar Partrtidge digantikan dengan Osprey yang mempunyai luas aluminium dalam milimeter persegi lebih dari dua kali. (b) jika suatu penghantar Partridge  kedua ditempatkan dalam suatu berkas  dua-penghantar 40 cm dari penghantar asli dan jarak antar-pusat berkas 5 m, dan (c) jika tegangan saluran asli ditingkatkan menjadi 230 kV dengan jarak pemisah penghantar dijauhkan menjadi 8 m.

Jawab :

Diketahui panjang saluran = 50 km, ini termasuk saluran pendek, dengan mengabaikan resistansinya maka konstanta-konstanta rangkaian umum adalah A=1A0° dan  B = XA90°. Juga pemanasan penghantarnya diabaikan, dari persamaan (5.59).

atau berbanding terbalik dengan X jika dimisalkan |V_S| dan |V_R| konstan.

D_eq = ∛(5 x 5 x 2 x 5) = ∛250 = 6.30 m atau

D_eq = (6.30/0.3048) = 20.67 ft

(a). Untuk penghantar Partridge dari daftar A1 D_S = 0.0217 ft

L = 2 x 10 ^-7 ln (D_eq/ D_S)         H/m

X_L = 2πf x 1000 x L                Ω/km

X_L = 4π60 x 1000 x 10 ^-7 ln (D_eq/ D_S)

X_L = 0.0754  ln (D_eq/ D_S) = 0.0754 ln (20.67/0.0217)

X_L = 0.5172 Ω/km

      Untuk penghantar  Osprey dari daftar A1 D_S = 0.0284 ft

X_L = 0.0754  ln (D_eq/ D_S) = 0.0754 ln (20.67/0.0284)

X_L = 0.4969 Ω/km

Perbandingan Daya yang diterima (P_R) baru dengan yang lama = (0.5172/0.4969) = 1.041.  
Sehingga peningkatan dayanya = [{(1.041-1)/1}x100] = 4.1%

(b). Jika penghantar berkas

ditempatkan dalam suatu berkas dua-penghantar 40 cm dari penghantar asli 
dan jarak antar-pusat berkas 5 m.     

Dari Daftar A1 untuk penghantar Partridge GMR = 0.0217 ft

D_S = √[0.0217 x {40/(100 x 0.3948}] = √0.0285 = 0.1688 ft

X_L = 0.0754  ln (D_eq/ D_S) = 0.0754 ln (20.67/0.1688)

X_L = 0.3625 Ω/km

Perbandingan Daya yang diterima (P_R) baru dengan yang lama = (0.5172/0.3625) = 1.427.  
Sehingga peningkatan dayanya = [{(1.427-1)/1}x100] = 42.7 %

(c). Jika tegangan ditingkatkan menjadi 230 kV dan jarak pemisah menjadi 8 m

Karena tegangan dinaikan maka daya yang diterima meningkat dengan faktor (230/138)² = 2.78.

D_eq = ∛(8 x 8 x 2 x 8) = ∛1024 = 10.08 m atau

D_eq = (10.08/0.3048) = 33.07 ft

X_L = 0.0754  ln (D_eq/ D_S) = 0.0754 ln (33.07/0.0217)

X_L = 0.5526 Ω/km

Daya yang diterima akan mengecil karena kenaikan reaktansi X

Dengan jarak pemisah lama 5 m   ===>            X_L = 0.5172 Ω/km

Dengan jarak pemisah baru 8 m   ===>            X_L = 0.5526 Ω/km

Faktor resultan kenaikan = 2.78 x (0.5172/0.5526) = 2.062

Sehingga peningkatan dayanya = [{(2.062-1)/1}x100] = 160.2 %

Disamping kenaikan pada jarak pemisah penghantar dan isolasi, mungkin diperlukan penghantar yang lebih besar karena arus akan meningkat dengan faktor kira-kira sebesar (230/138) = 1.67 dan rugi |I|².R dalam saluran kira-kira dengan faktor 2.78 untuk kenaikan pada beban dengan faktor daya yang sama.

5.14     Gambarkanlah diagram lingkaran-daya seperti Gambar 5.10 untuk ujung penerima saluran yang diberikan dalam Soal 5.8. Tentukanlah titik yang sesuai dengan beban pada Soal 5.8 tersebut, dan tentukan juga titik-tengah lingkaran-lingkaran untuk bermacam-macam nilai │V_S │jika │V_R│= 220 kV. Gambarkan lingkaran yang melewati titik beban. Dengan mengukur jari-jari lingkaran ini, tentukan │V_S │, dan bandingkan nilai dengan nilai-nilai yang dihitung pada Soal 5.8

Jawab :

Skala  1 inci : 50 MVA

Persamaan V_S = A V_R + B I_R , data dari Soal 5.8 (c). :      

A = 0.9354 + j 0.0160 = 0.9355 A0.98°

B = 394 A- 7.02° x( 0.0419 + j 0.3565) = 141.4 A76.28°

β – α = 76.28° - 0.98° = 75.3°

Cos θ = 0.9    ==>  θ = 25.8°

Panjang 0-n = 320/50 = 6.4 inci dengan sudut 75.3°

Tarik garis beban melalui titik 0 dengan sudut θ = 25.84°, kemudian tarik garis tegak pada skala daya 40 MW dan bersilangan dengan garis beban pada titik k yang disebut titik beban. Dan ukur radius lingkaran yang lewat titik beban, n-k adalah 7.05 inci = 7.05 x 50 = 352.5 MVA ini adalah :

 

(dibandingkan dengan hasil perhitungan dalam Soal 5.8 (c). |V_S| = 225.4 kV)

5.15     Gunakan diagram yang digambar dalam Soal 5.14 untuk menentukan tegangan ujung pengirim untuk bermacam-macam nilai kilovar yang diberikan oleh kondensator-kondensator sinkron yang terhubung paralel dengan beban yang disebutkan pada ujung penerima. Masukkan nilai-nilai kilovar yang ditambahkan untuk memberi faktor daya satu dan faktor daya 0,9 mendahului pada ujung penerima. Misalkan bahwa tegangan ujung pengirim diatur sedemikian sehingga tegangan pada beban tetap 220 kV.

Jawab :

Pada diagram untuk soal 5.14 gambarkan sebuah garis beban baru pada kwadran ke empat yang mempunyai sudut arc cos 0.9 atau θ = 25.84° dengan sumbu mendatar. Gambarkan lingkaran-lingkaran daya dengan radius-radius :

berturut-turut untuk |V_S| = 200, 210, 220, 230, 240 dan 250 kV. 
Untuk faktor daya = 1.0 bacalah |V_S| = 214 kV pada 40 MW pada sumbu mendatar dari garis beban pada kwadran pertama merepresentasikan kVAR dari kondensor-kondensor sinkron atau kapasitor-kapasitor yang diperlukan. Nilai ini adalah 19.3 kVAr.

Untuk faktor daya = 0.9 medahului bacalah V_S = 202 kV dimana garis tegak lewat 40 MW memotong garis beban dalam kwadran ke empat. Jarak tegak diantara kedua garis –garis beban pada 40 MW merepresentasikan kVar dari kondesor-kondensor sinkron atau kapasitor yang diperlukan adalah 38.6 kVar.

5.16     Suatu diagram lingkaran-daya ujung penerima digambar untuk suatu tegangan ujung penerima yang konstan. Untuk suatu beban tertentu pada tegangan ujung penerima ini, tegangan ujung pengirim adalah 115 kV. Lingkaran ujung penerima untuk │V_S │= 115 kV mempunyai jari-jari sepanjang 5 in. Koordinat-koordinat mendatar dan tegak dari lingkaran-lingkaran ujung penerima berturut-turut adalah – 0,25 dan – 4,5 in. Hitunglah regulasi tegangan beban.

Jawab :

Pada keadaan tanpa beban V_S = A . V_{R, tanpa beban}

 

 

5.17     Suatu saluran transmisi tiga-fasa sepanjang 300 mi melayani beban sebesar 400 MVA dengan faktor daya 0,8 tertinggal pada tegangan 345 kV. Konstanta-konstanta ABCD saluran adalah

A = D =  0.8180 A1.3°

B = 172.2 A84.2° Ω

C =  0.001933 A90.4° ℧

(a) Tentukan tegangan antara saluran dan netral di ujung pengirim, arus ujung pengirim dan persentase jatuh tegangan pada beban penuh.

(b) Tentukan  tegangan antara saluran dan netral di ujung penerima pada keadaan tanpa beban, arus ujung pengirim pada keadaan yang sama dan regulasi tegangan.

Jawab :

Faktor Daya tertinggal (cos θ ) = 0.8  ====> θ = 36.87°

(a).       V_S = A V_R + B I_R                   I_S = C V_R + D I_R

V_S = 0.8180 A1.3° x 199 186 A0° + 172.2 A84.2° x 669.4 A-36.87°

V_S = 162 934.15 A1.3° + 115 270.7 A47.33°

V_S = 162 892.2 + j 3696.5 + 78 127.6 + j 84755

V_S = 241 019.8 + j 88451.5

V_S = 256 737.6 A 20.15° ≈ 256 738 A 20.15° V ke netral

I_S = 0.001933 A90.4° x 199 186 A0° + 0.8180 A1.3° x 669.4 A-36.87°

I_S = 385.03 A90.4° + 547.6 A-35.57°

I_S = - 2.688 + j 385.03 + 445.4 – j 318.54

I_S = 442.712 + j 66.49

I_S = 447.7 A8.5° A

(b).     Keadaan tanpa beban :  

          V_{R, tanpa beban}  = (V_S/A)

I_{S,tanpa beban} = C V_{R, tanpa beban}  

I_{S,tanpa beban} = 0.001933 A90.4° x 313 861 A18.85°

I_{S,tanpa beban} = 606.7 A109.25° A

5.18     Suatu bank kapasitor seri akan dipasang di tengah-tengah saluran 300 mi yang dilukiskan dalam Soal 5.17. Konstanta ABCD untuk saluran 159 mi. adalah  

A = D =  0.9534 A0.3°

B = 90.33 A84.1° Ω

C =  0.001014 A90.1°℧

Konstanta ABCD dari bank kapasitor seri adalah

A = D =  1 A0°

B = 146.6 A- 90° Ω

C =  0

(a) Tentukanlah konstanta ABCD ekivalen dari gabungan seri saluran-kapasitor-saluran.(Lihat Daftar A.6 
      dalam Appendix).

(b) Kerjakan kembali Soal 5.17 dengan menggunakan konstanta ABCD ekivalen.

Jawab :

(b). V_R  dan I_R diambil dari jawaban Soal 5.17

V_S = A V_R + B I_R

V_S = 0.9597 A1.18° x 199 186 A0° + 42.3 A64.5° x 669.4 A-36.87°

V_S = 191158.8 A1.18°  + 28315.62 A27.63°

V_S = 191118.3 + j 3936.6 + 25086.53 + j 13131.65

V_S = 216 204.83 + j 17068.25

V_S = 216 878 A4.5° V

I_S = C V_R + D I_R

I_S = 0.002084 A90.4° x 199 186 A0° + 0.9597 A1.18° x 669.4 A-36.87°

I_S = 415.1036 A90.4° + 642.423 A-35.69°

I_S = - 2.8979 + j 415.0935 + 521.767 – j 374.789

I_S = 518.8688 + j 40.3042

I_S = 520.43 A4.44° A

(dibandingkan dengan Soal 5.17        V_D = 22.4 %)

Keadaan tanpa beban I_R = 0

   









 

I_{S,tanpa beban} = C V_{R, tanpa beban}  

I_{S,tanpa beban} = 0.002084 A90.4° x 225 985 A3.32°

I_{S,tanpa beban} = 470.95 A93.72° A 

(dalam Soal 5.17 .Sedangkan saluran tanpa kapasitor-kapasitor regulasi tegangan = 57.6 % )

5.19     Admitansi shunt suatu saluran transmisi sepanjang 300 mi adalah

                        Y_c = 0 + j6.87 x 10 ^{– 6} ℧ /mi.

Tentukanlah konstanta ABCD suatu reaktor shunt yang akan memberikan kompensasi sebesar 60% dari admitansi shunt total.

Jawab :

Admitansi shunt total atau Suseptansi kapasitif

B_C = 300 ( j 6.87 x 10 ^{– 6}) = 0.002061 ℧

Untuk kompensasi 60 % atau Suseptansi induktif

B_L = - j 0.6 x 0.002061 = - j 0.001237 ℧

Jadi kontanta ABCD reaktor shunt adalah ;

A = D = 1A0°

B = 0

C = - j 0.001237 ℧

5.20    Suatu reaktor shunt 250 MVAR, 345 kV yang admitansinya adalah 0.0021A- 90°℧ Dihubungkan pada ujung penerima saluran 300 mi pada Soal 5.17 dalam keadaan tanpa beban.

(a) Tentukanlah konstanta ABCD ekivalen dari saluran yang terhubung seri dengan reaktor shunt (Lihat    
      Daftar A.6 dalam Appendix).

(b) Kerjakan kembali bagian (b) dari Soal 5.17 dengan menggunakan konstanta ABCD ekivalen ini dan 
      tegangan ujung pengirim yang telah ditemukan dalam Soal 5.17.

Jawab :

Konstanta ABCD saluran pada Soal 5.17 adalah :

A₁ = D₁ = 0.8180 A1.3°  ; B₁ = 172.2 A84.2° Ω ; C₁ = 0.001933 A90.4° ℧

Dipasang reaktor shunt yang mempunyai konstanta ABCD ialah :

A₂ = D₂ = 1A0° ; B₂ = 0 ; C₂ = 0.0021 A-90° ℧

(a). Konstanta ekivalen dari saluran yang terhubung seri dengan raktor shunt tersebut :

A_ekivalen = A₁.A₂ + B₁.C₂ = 0.8180A1.3° x 1 A0° + 172.2 A84.2° x 0.0021 A-90°

A_ekivalen = 0.8180 A1.3° + 0.36162 A-5.8°

A_ekivalen = 0.8177895 + j 0.0185582 + 0.35976876 – j 0.0365434

A_ekivalen = 1.1775583 – j 0.0179852 = 1.1777 A- 0.88°

B_ekivalen = A₁.B₂ + B₁.D₂ =  0.8180 A1.3° x 0 + 172.2 A84.2° x 1 A0°

B_ekivalen = 172.2 A84.2°

C_ekivalen = A₂.C₁+C₂.D₁ =1A0° x 0.001933A90.4° + 0.0021A-90° x 0.8180A1.3°

C_ekivalen = 0.001933 A90.4° + 0.0017178 A-88.7°

C_ekivalen = - 0.000013494 + j 0.001932952 + 0.000038972 – j 0.00171736

C_ekivalen = 0.000025478 + j 0.000215592

C_ekivalen = 0.000217 A83.26°

D_ekivalen = B₂.C₁ + D₁.D₂ = 0 x 0.001933 A90.4° + 0.8180 A1.3° x 1 A0°

D_ekivalen = 0.8180 A1.3°

(b). Dari Soal 5.17 diperoleh V_S = 256 738 A20.15° V

Pada keadaan tanpa beban I_R = 0

I_{S,tanpa beban} = C V_{R, tanpa beban}  

I_{S,tanpa beban} = 0.000217 A83.26° x 217 999A21.03°

I_{S,tanpa beban} = 47.306 A104.29° A

Perlu diketahui bahwa reaktor shunt hanya berada dalam rangkaian pada keadaan tanpa beban, jadi dari hasil Soal 5.17 V_{R,beban penuh} = 199 186 A0° V.

(dibandingkan dalam Soal 5.17 Regulasi Tegangan = 57.6 %)

5.21     Gambarkan diagram terali untuk arus dan lukiskan grafik arus terhadap waktu pada ujung pengirim saluran dalam Contoh 5.6 untuk saluran yang ditutup dengan (a) suatu rangkaian terbuka dan (b) suatu hubungan singkat.

Jawab :

Diketahui sumber V = 120 V dihubungkan pada saluran transmisi yang mempunyai Z_C = 30 Ω.

5.22     Lukiskan grafik tegangan terhadap waktu untuk saluran dalam Contoh 5.6 pada suatu titik yang terletak sejauh seperempat panjang saluran dari ujung pengirim, jika saluran ditutup dengan tahanan sebesar 10 Ω.

Jawab :

Pada diagram dari gambar 5.15 b ditarik garis bayangan pada seperempat panjang saluran dari ujung pengirim ke arah ujung penerima.

Perpotongan garis tsb dengan garis miring terjadi pada T = 0.25T; 1.75T; 2.25T; 3.75T; dst. Perubahan – perubahan tegangan terjadi pada waktu – waktu ini. Jumlah dari tegangan-tegangan yang datang dan yang dipantulkan digambarkan diantara garis-garis miring dan menentukan nilai-nilai yang dipetakan di bawah ini.

5.23     Selesaikan Contoh 5.6 jika suatu tahanan sebesar 54 Ω terhubung seri dengan sumber.

Jawab :

Untuk tegangan :

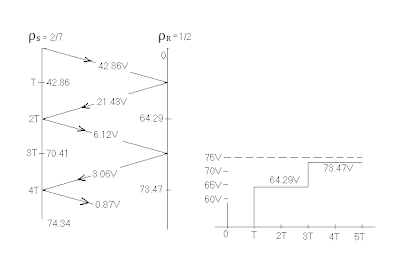
ρ _S = {(54 – 30)/(54 + 30)} = 2/7   

ρ _R = {(90 + 30)/(90 +30)} = 1/2

tegangan mula-mula yang di masukkan ke saluran :

{30/(30+54)} x 120 = 42.86 V

Periode T                                   = 42.86          V

Pantulan ρ_R = 42.86 x ½         = 21.43          V

Periode 2T = 42.86 + 21.53   = 64.29          V

Pantulan ρ_s  = 21.43 x 2/7     = 6.12             V

Periode 3T = 64.29 + 6.12     = 70.41          V

Pantulan ρ_R  = 6.12 x ½         = 3.06             V

Periode 4T = 70.41 + 3.06     = 73.47          V

Pantulan ρ_s    = 3.06 x 2/7     = 0.87             V

Periode 5T = 73.47 + 0.87    = 74.34          V

 

Tegangan terakhir adalah :

{90/(90+54)} x 120 = 75 V

5.24     Tegangan dari suatu sumber dc dikenakan pada suatu saluran transmisi atas-tiang dengan menutup sebuah sakelar. Ujung saluran atas-tiang tersebut dihubungkan pada suatu kabel bawah tanah. Misalkan bahwa baik saluran maupun kabel adalah tanpa rugi dan bahwa tegangan awal pada saluran adalah v⁺ . Jika impedansi karakteristik saluran dan kabel berturut-turut adalah 400Ω dan 50Ω, dan ujung kabel merupakan rangkaian terbuka, nyatakanlah dengan menggunakan v⁺ sebagai suku-sukunya (a) tegangan pada titik sambungan antara saluran dan kabel segera setelah tibanya gelombang datang  dan (b) tegangan pada ujung kabel yang terbuka segera setelah datangnya gelombang tegangan yang pertama.

Jawab :

Gelombang tegangan permulaan v_o⁺ yang sampai  pada sambungan dengan kabel.

Sehingga di ujung saluran di atas tiang tersebut :   ρ _R = {(50 – 400)/(50 + 400)} = 0.777.

(a). Tegangan pada titik sambungan adalah : (1 – 0.777)v⁺ = 0.223 v_o⁺ 
         ini merupakan gelombang tegangan yang dibiaskan (refracted) di sepanjang kabel.   

(b). Tegangan pada  ujung kabel :   ρ _R = 1  (rangkaian terbuka) dan

        v_R = (0.223 + 0.223)v⁺ = 0.446 v_o⁺ .

ooomsooo