Permeabilitas
Magnet
Daya hantar atau permeabilitas magnet μ merupakan
parameter bahan yang menentukan besarnya fluks magnetik.
Permeabilitas ruang
kosong μo telah terpilih
sebagai konstanta referensi.
μo
= 1,256 . 10-6 [Weber/ampere x
meter] (Wb/Am atau H/m)
Dalam sistem satuan elektromagnet
yang lama μo bernilai
μo =
1,256 [Gauss x sentimeter/ampere] (G•cm/A)
Permeabilitas μ dari setiap bahan
yang lain dinyatakan sebagai kelipatan μo .
Pengganda dinamakan permeabilitas relatif μr, sehingga
μ = μo • μr
Untuk kebanyakan bahan μr,
harganya mendekati satu, hingga permeabilitasnya praktis sama dengan μo
.
Pengecualian terhadap keadaan ini
ialah bahan feromagnetik;
permeabilitas relatif μr jenis bahan tersebut jauh lebih besar
daripada satu.
Bahan-bahan feromagnetik adalah
Kobalt μr sampai 70
Nikel μr sampai 200
Besi
dan besi paduan μr` sampai 100.000
Disebabkan oleh nilai
permeabilitasnya yang tinggi, bahan feromagnetik dipergunakan untuk rangkaian
magnet, umpamanya untuk magnet listrik (elektromagnet) dalam mesin listrik dan
transformator.
Rangkaian
Magnet
Jejak tertutup arus listrik
dinamakan “ Rangkaian Listrik “ (Gambar
16)
Sehubungan dengan itu jejak
tertutup untuk fluks magnetik
dinamakan “ Rangkaian Magnet “ (Gambar 17)
Parameter-parameter berikut ini adalah ekuivalen (setara):
Tahanan Ohm R Reluktansi
magnet RM
Arua Listrik I Fluks
Magnetik Φ
Gaya Gerak Listrik atau Gaya
Gerak Magnetis atau
GGL E yang menggerakkan GGM
θ yang menimbulkan
arus melalui rangkaian fluks
magnetik
Perbandingan
Rangkaian Magnet dan Rangkaian Listrik
Kita telah melihat bahwa
“rangkaian listrik” dan “rangkaian magnet” adalah ekuivalen (setara). Oleh
sebab itu hubungan matematika dalam kedua rangkaian harus serupa.
Marilah kita pergunakan diagram
rangkaian yang sama untuk kedua rangkaian:
Rangkaian Listrik Rangkaian Magnet
GGL E menggerakkan arus I GGM θ menghasilkan
fluks magnetik
melalui tahanan Ohm R. melalui
reluktansi magnet RM.
Kita memiliki Hukum Ohm untuk Kita memiliki Hukum Ohm
untuk
Sebagai contoh tentang penerapan
Hukum Ohm pada rangkaian magnet, kita akan menentukan GGM yang dibutuhkan untuk
menginduksi B sebesar 50 • 10-4 T (Tesla) pada bagian sebelah dalam
kumparan bentuk gelang yang memiliki teras (inti) udara sebagaimana terlihat
pada Gambar 20.
Garis tengah rata-rata gelang
D = 30 cm,
jadi panjang jejak fluks ℓ :
ℓ = D•π = 30 • π cm
ℓ = 94,2 cm = 0,942 m
Garis tengah kumparan d = 3 cm,
jadi luas bidang A:
A = d2 • (π/4) = 32 • (π/4) = 7,06 cm2
= 7,06 • 10-4 m2
Penyelesaian :
Sesuai dengan Hukum Ohm untuk rangkaian magnet:
Θ = RM • Φ
(1)
Maka kita harus menentukan fluks magnetik Φ dan reluktansi RM
Φ = B•A
Φ = 50x10-4 x 7,06x10-4
Θ = 353x10-8 x 10,6x108 AT
Θ = 3740 AT (Ampere –Turns)
Permeabilitas
Besi
Reluktansi jejak fluks magnetik dalam udara memiliki nilai konstan tertentu yang diberikan oleh :
karena μo konstan.
Keadaan ini tidak berlaku untuk
jejak fluks magnetik dalam besi,
berubah dengan μ yang tidak konstan.
Reluktansi itu berubah-ubah menurut pola yang terlihat pada grafik
di bawah ini (Gambar 21)
Bila besi sedikit dimagnetkan
yaitu induksi magnet B dalam besi hampir nol, permeabilitas memiliki nilai-awal
tertentu μA, yang
tergantung dari jenis besi yang dipergunakan.
Dengan memperbesar induksi
magnet, permeabilitas besi naik sampai μ mencapai maksimum pada induksi magnet
B1. Jika induksi magnet ditingkatkan lebih lanjut, μ turun dengan
cepat sekali dan mulai B2 malahan menjadi lebih rendah daripada
nilai-awal μA.
Karena itu untuk menentukan GGM θ
suatu rangkaian magnet yang mengandung besi, Kita harus menggunakan pendekatan
yang berbeda.
Beda
Potensial Magnet
Marilah kita bandingkan lagi
rangkaian listrik dengan rangkaian magnet, akan tetapi kali ini dengan dua buah
tahanan yang berbeda dalam rangkaian listrik dan dua buah reluktansi yang
berbeda dalam rangkaian magnet (Gambar 22 dan 23).
Rangkaian arus listrik : Rangkaian
magnet :
GGL E menggerakkan arus I GGM θ menghasilkan
fluks
melalui rangkaian. magnetik
Φ dalam rangkaian.
“Beda potensial listrik” U1 “Beda
potensial magnet” V1
dan U2 timbul pada R1
dan R2 dan
V2 timbul dalam RM1 dan RM2
U1 = I•R1 ;
U2 = I•R2 V1
= Φ•RM1 ; V2 =
Φ•RM2
Jadi untuk seluruh rangkaian kita
Jadi untuk seluruh
rangkaian kita
memiliki E = U1 + U2 memiliki θ =
V1 + V2
Karena itu beda potensial magnet
V ialah bagian dari GGM θ total yang terdapat pada suatu seksi jejak magnet
dari rangkaian magnet.
Satuan beda potensial magnet ialah ampere (A).
Dalam sistem satuan elektromagnet
yang lama, satuan beda potensial magnet ialah Gilbert (Gb). Untuk konversinya
kita memiliki :
1 A = 1,256 Gb
Kuat
Medan Magnet
Hampir setiap rangkaian magnet
terdiri dari sejumlah reluktansi magnet yang berbeda-beda.
Untuk
menyederhanakan perhitungan dalam rangkaian semacam itu kita masukkan suatu
parameter yang berlaku sama untuk setiap reluktansi dalam rangkaian, ini
berarti untuk semua bagian jejak fluks magnetik.
Parameter ini ialah kuat
medan magnet H.
Setiap reluktansi magnet
mempunyai ukuran panjang yang tertentu, yang sesuai dengan bagiannya dari jejak
fluks magnetik.
Beda potensial magnet yang timbul terbagi rata sepanjang
reluktansi tersebut.
Resultan beda potensial magnet per satuan panjang
rangkaian magnet ialah
kuat medan magnet
H.
Satuan dari kuat medan magnet sama dengan Ampere/m, yaitu A/m atau AT/m.
Satuan dalam sistrem satuan
elektromagnet yang lama adalah Oersted (Oe).
Untuk konversinya : 1 A/m =
0,01256 Oe.
Bila suatu kuat medan magnet H
akan dihitung untuk sebagian rangkaian magnet, maka beda potensial magnet pada
bagian tersebut akan diberikan oleh
V
= H • ℓ
Hubungan antara Kuat Medan Magnet dan Induksi Magnet
Dalam banyak hal yang diketahui
bukanlah medan magnet H untuk sebagian dari rangkaian magnet, akan tetapi
induksi magnet B. Oleh sebab itu kita harus menentukan hubungan antara H dan B. Hal ini ditetapkan oleh persamaan:
Persamaan ini menyatakan kepada kita, bahwa makin tinggi induksi magnet B (yang merupakan kerapatan fluks magnetik) yang dibangkitkan oleh suatu kuat medan magnet H, makin tinggi pula permeabilitas bahan rangkaian magnet.
V = Φ • RM
Bila ketiga suku diganti dengan :
V = H • ℓ
Φ = B •A
Maka kita peroleh
atau B = μ • H
Persamaan ini menyatakan kepada kita, bahwa makin tinggi induksi magnet B (yang merupakan kerapatan fluks magnetik) yang dibangkitkan oleh suatu kuat medan magnet H, makin tinggi pula permeabilitas bahan rangkaian magnet.
Untuk medan magnet dalam udara
kita memiliki
atau B =μo • H
atau B = μr • μo • H
Kurva Pemagnetan untuk Bahan Feromagnetik
atau B = μr • μo • H
Kurva Pemagnetan untuk Bahan Feromagnetik
Bila medan magnet digunakan untuk
membangkitkan gaya mekanis, umpamanya dalam magnet-angkat atau motor listrik,
selalu diperlukan induksi magnet B yang besarnya tertentu untuk menghasilkan
gaya mekanis tersebut.
Bagi perancang rangkaian magnet, maka perlu untuk
menetapkan kuat medan magnet H dan karena itu banyaknya gulungan ampere yang
dibutuhkan untuk menghasilkan induksi magnet B yang sesuai.
Pengukuruan telah dilakukan
terhadap banyak contoh bahan feromagnetik yang digunakan dalam bidang teknik.
Tujuannya untuk menetapkan hubungan yang eksak antara kuat medan magnet H dan
induksi magnet B, untuk bahan besi tertentu.
Nilai-nilai yang terukur dari
semua contoh ini kemudian digambarkan pada sebuah grafik, guna membuat kurva
pemagnetan jenis besi bersangkutan.
Kurva tersebut memberi jalan bagi kita
untuk membaca kuat medan magnet H untuk setiap nilai induksi magnet B yang
diinginkan.
Gambar 24 memperlihatkan contoh
kurva pemagnetan untuk besi tuang dan baja lembaran transformator, dua bahan
feromagnetik yang di pergunakan dalam mesin listrik atau transformator.
Penggunaan
Kurva Pemagnetan
Sebagai contoh tentang bagaimana
cara menggunakan kurva pemagnetan, marilah kita hitung data untuk sebuah
kumparan eksitasi yang digulung pada teras (inti) besi tuang sebagaimana yang
diperlihatkan pada Gambar 25.
Induksi magnet yang dibutuhkan
ialah 0,5 Tesla.
Kita perlu menghitung kuat medan magnet H dan GGM θ dan
kemudian ditetapkan arus yang masuk ke kumparan dan banyaknya gulungan pada
kumparan.
Dari kurva pemagnetan untuk besi
tuang (Gambar 24) kita peroleh (garis putus-putus) :
B = 0,5 Tesla, Besi tuang H =
1600 AT/m
Dari Gambar 25 kita tentukan
panjang rata-rata jejak magnet
ℓ = 30 + 30 + 20 + 20 cm = 100 cm
= 1 m
Maka
θ
= H • ℓ = 1600•1 = 1600 AT
Perkalian arus dan banyaknya gulungan ini memberi kemungkinan kepada kita untuk memilih 1600 gulungan dan 1 A atau 800 gulungan dan 2 A atau 400 gulungan dan 4 A atau 200 gulungan dan 8 A dan seterusnya.
( Bersambung......)











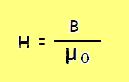


Kayak sinetron za bersambung Gan ...makasih ilmunya
BalasHapusTulisannya sistematis, konsep fisisnya mudah dimengerti, keren. Jazakalloh Khoiran Katsiran
BalasHapusSemangat terus berkarya Om !!!
Amien...semoga bermamfaat....terimakasih
BalasHapusSimple,, mudah dipahami dan sangat membantu tugas saya...
BalasHapus